Demonstration of the thermodynamic principle dominant configuration using coin flips.

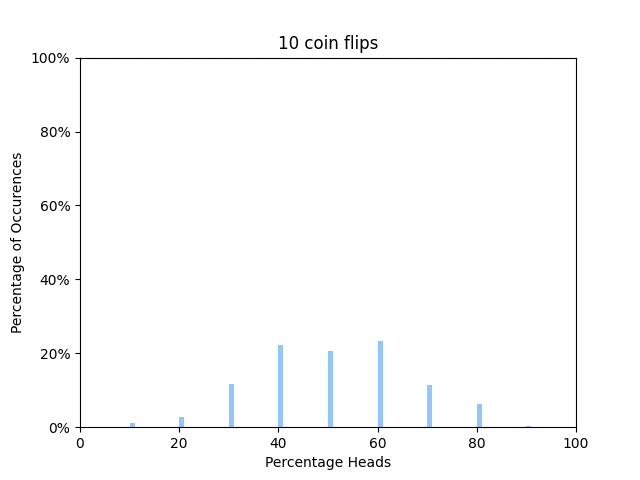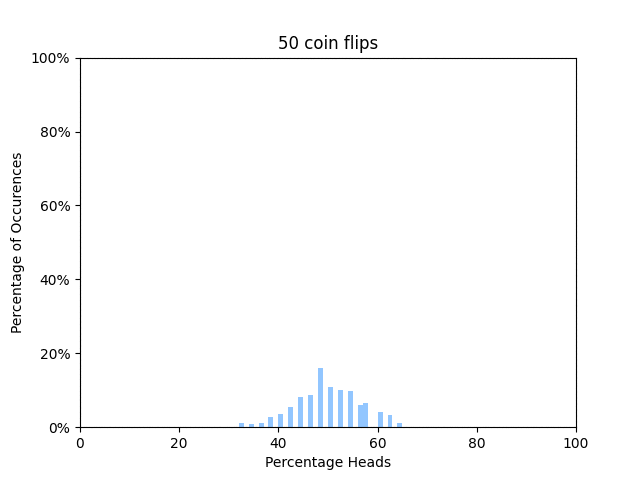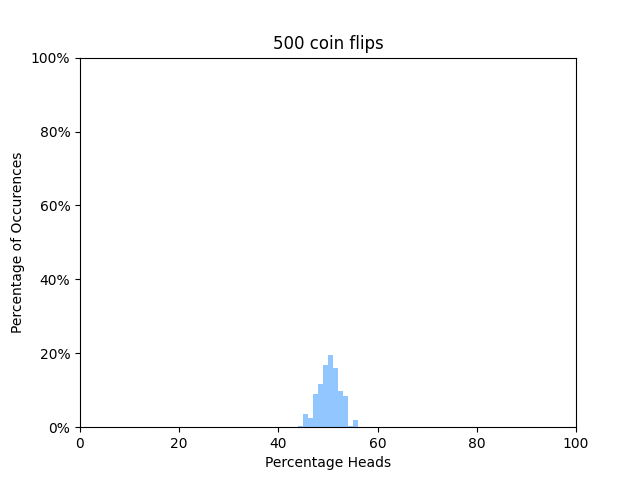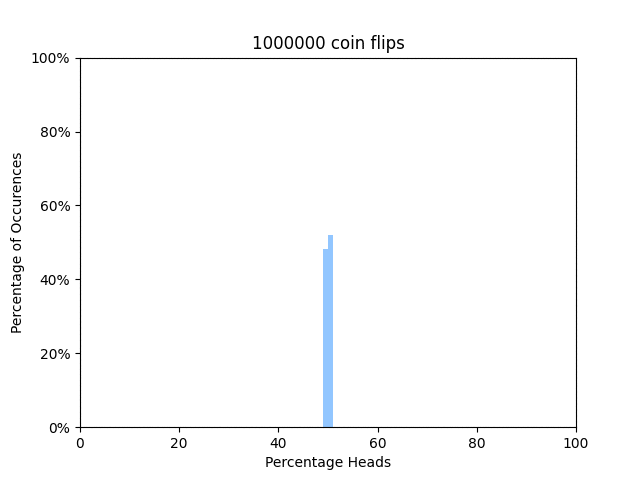
In statistical thermodynamics, the dominant configuration is the state in which a system is most likely to be found. This idea can be compared to flipping a coin. If you flip a coin 4 times, there’s only 1 case where you could get 0 heads. To get 1 head, you could have the first flip be a head, then the rest be tails, or, you could have the first toss be a tails, the second a heads, and the remaining two be tails. Going through the rest of this scenario, you would find there is 1 way to get 0 heads, 4 ways to get 1 heads, 6 ways to get 2 heads, 4 ways to get 3 heads, and 1 way to get 4 heads. If we were to scale this up to the magnitude of the number of particles found in say a room, which is on the order of 10^23, then you would most certainly find that you will get 50% the number of heads as number of tosses. The figure above demonstrates this, as the peak gets narrower and narrower around 50% as the number of tosses goes up. Even at a million tosses, the peak is almost fully concentrated around 50% heads. Applying this concept to a macroscopic system of particles, the dominant configuration will be so likely that it can be chosen to definet the properties of the system.

This python script simulates flipping a coin by choosing a 0 or a 1 with 50% probability of either. It then “flips” a coin a specified number of times and plots the results to a histogram.

GitHub